Потенциал электрического диполя
Публикации по материалам Д. Джанколи. "Физика в двух томах" 1984 г. Том 2.
 Два равных по величине и противоположных по знаку точечных заряда Q, находящиеся на расстоянии r друг от друга, называются электрическим диполем. Силовые линии и эквипотенциальные поверхности диполя показаны в предыдущей публикации на рис. 24.3.
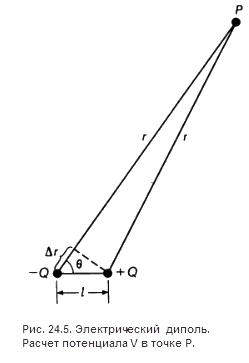
Рассчитаем электрический потенциал, создаваемый диполем в произвольной точке Р (рис. 24.5). Потенциал V представляет собой сумму потенциалов, создаваемых каждым из зарядов:
Два равных по величине и противоположных по знаку точечных заряда Q, находящиеся на расстоянии r друг от друга, называются электрическим диполем. Силовые линии и эквипотенциальные поверхности диполя показаны в предыдущей публикации на рис. 24.3.
Рассчитаем электрический потенциал, создаваемый диполем в произвольной точке Р (рис. 24.5). Потенциал V представляет собой сумму потенциалов, создаваемых каждым из зарядов:
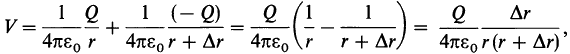
где r - расстояние от точки Р до положительного заряда, а r + Δr - до отрицательного заряда. Выражение упростится, если рассматривать точки, расстояние которых до диполя гораздо больше расстояния между зарядами, когда r значительно больше l . Как видно из рисунка, в этом случае Δr ≈ lcosθ;
тогда r будет значительно больше Δr = lcosθ, и в знаменателе величиной Δr можно пренебречь по сравнению с r. Такого рода приближения часто оказываются полезными и позволяют получить простое выражение для потенциала
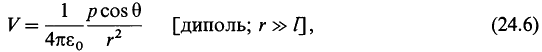
где р = Ql - дипольный момент. При 0° < θ < 90° потенциал V положителен, при 90° < 0 < 180° потенциал
отрицателен (поскольку отрицательно значение cosθ). Это разумно, поскольку в первом случае точка Р ближе к положительному заряду, а во втором-к отрицательному. При 0 = 90° потенциал равен нулю (cos 90° = 0) в соответствии с результатом примера 24.4. Из (24.6) мы видим, что потенциал убывает как квадрат расстояния до диполя, в то время как потенциал точечного заряда убывает как первая степень расстояния [см. (24.5)].
Это неудивительно: на больших расстояниях от диполя заряды кажутся столь близкими друг к другу, что взаимно нейтрализуются.
Во многих молекулах, в целом электрически нейтральных, электроны проводят больше времени у одного атома, чем у другого, что эквивалентно разделению зарядов. Такие молекулы обладают дипольным моментом и называются полярными.
Зная напряженность электрического поля, создаваемого данным распределением зарядов, можно рассчитать разность потенциалов между любыми двумя точками, пользуясь формулой (24.4). Но нередко поле Е неизвестно и его сложно рассчитать. Потенциал любого распределения
зарядов можно получить иным и часто более простым способом, вычисляя потенциалы, создаваемые каждым точечным зарядом
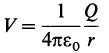 и затем суммируя их.
и затем суммируя их.
Если имеется n точечных зарядов, то потенциал в некоторой точке c равен
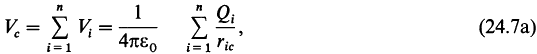
где ric - расстояние от i-го заряда Qi до точки c. Такой подход использовался в примере 24.4 Джанколи для случая диполя (разд. 24.6). Если распределение зарядов можно считать непрерывным, тогда:

где r - расстояние от элемента заряда dq до точки, в которой определяется V.
Продолжение следует. Коротко о следующей публикации:
Определение напряженности электрического поля Е с помощью потенциала V.
Составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом потенциала V называется его производная по определенному направлению dV/dl.
Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения потенциала.
Альтернативные статьи:
Постоянный ток, Переменный ток.
Замечания и предложения принимаются и приветствуются!