Электрический импеданс
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение

При последовательном соединении, согласно Закону Ома для переменного тока,
во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL - UC .
Пропорционально напряжению, получим общее реактивное сопротивление X = XL - XC .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.

Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах,
определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
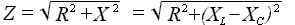
XL = ωL = 2πfL - реактивное сопротивление индуктивности.
XC = 1/(ωC) = 1/(2πfC) - реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:

Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа,
где действительной его частью является активное сопротивление, а мнимой - реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
Z = R + jX
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом - угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
Z = |Z|ejargZ = Zejφ
Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение

Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин - проводимостей y = 1/Z, G = 1/R, b = 1/X.
y = 1/Z = √(G2 + b2)
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:

Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Y = G - jb
Либо в показательной форме:
Y = |Y|e -jφ = ye -jφ
Здесь:
Y - комплексная проводимость.
G - активная проводимость.
b - реактивная проводимость.
y - общая проводимость цепи, равная модулю комплексной проводимости.
e - константа, основание натурального логарифма.
j - мнимая единица.
φ - угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
|
Последовательное соединение Z = √(R²+(XL-Xc)²) |
Параллельное соединение Z = 1/√(1/R²+(1/XL-1/Xc)²) |
Похожие страницы с расчётами:
Реактивное сопротивление. Расчёт.